The algebraic identity (a + b)² = a² + 2ab + b² is a foundational formula in mathematics, commonly used in algebraic expansion and simplification. It helps in understanding polynomial multiplication and lays the groundwork for more complex algebraic manipulations. In this article, we’ll demonstrate how to implement this equation using a SQL Server stored procedure that takes two input values (a and b) and computes the expanded result.
Below is the code of Stored Procedure:
/********************************************************************
Purpose: To evaluate the equation (a + b)² = a² + 2ab + b² using SQL
Input Parameters: @a INT, @b INT
Output Parameter: @Result INT
********************************************************************/
alter PROCEDURE dbo.EvaluateBinomialSquare
@a INT,
@b INT,
@Result INT OUTPUT
AS
BEGIN
SET @Result = POWER(@a, 2) + 2 * @a * @b + POWER(@b, 2)
END
GO
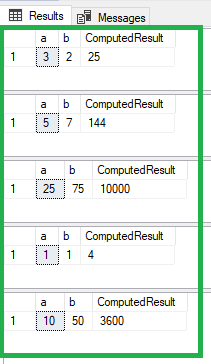
Execution of Stored Procedure:
DECLARE @a FLOAT = 3;
DECLARE @b FLOAT = 2;
DECLARE @Output FLOAT;
EXEC dbo.EvaluateBinomialSquare @a, @b, @Result = @Output OUTPUT;
SELECT @a as 'a', @b as 'b', @Output AS ComputedResult;
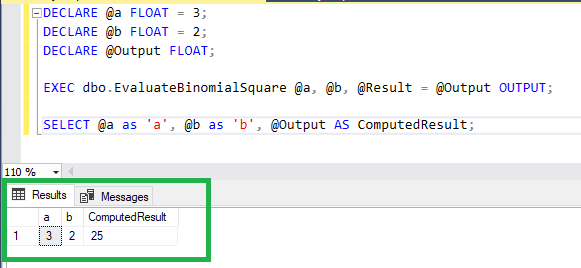
Following are some more results: